树状数组(BIT)

树状数组是一种支持单点修改和区间查询的，代码量小的数据结构,在这里我们可以理解为线段树的简化版本

• 树状数组对单点修改和区间查询的时间复杂度都为$O(\log n)$
• 对于前缀和，树状数组在更新值的时候

引入

对于数组 $A$ 其中元素为 [$a_0,a_1\cdots a_n$]
有$q$次询问，每次询问可能涉及两种操作

• 对 $a_i$ 加 $k$
• 给定区间$[l,r]$，求区间和

• 对数组$A$，我们朴素的使用前缀和也可以实现上面的两个操作，但是对于询问次数特别多且$n$特别大的时候，前缀和在修改的$O(n)$时间复杂度就不能满足题目要求

• 我们试想，将$A$的每个元素两两加和得到一个新的$A^{\prime }$，对$A^{\prime }$做操作这样我们需要查询和修改的$n$就变为了 $\frac{n}{2}$

• 我们继续重复以上步骤，将每次的$A^{\prime }$的元素都两两加和

• 最终我们会得到下面的一幅图：
  

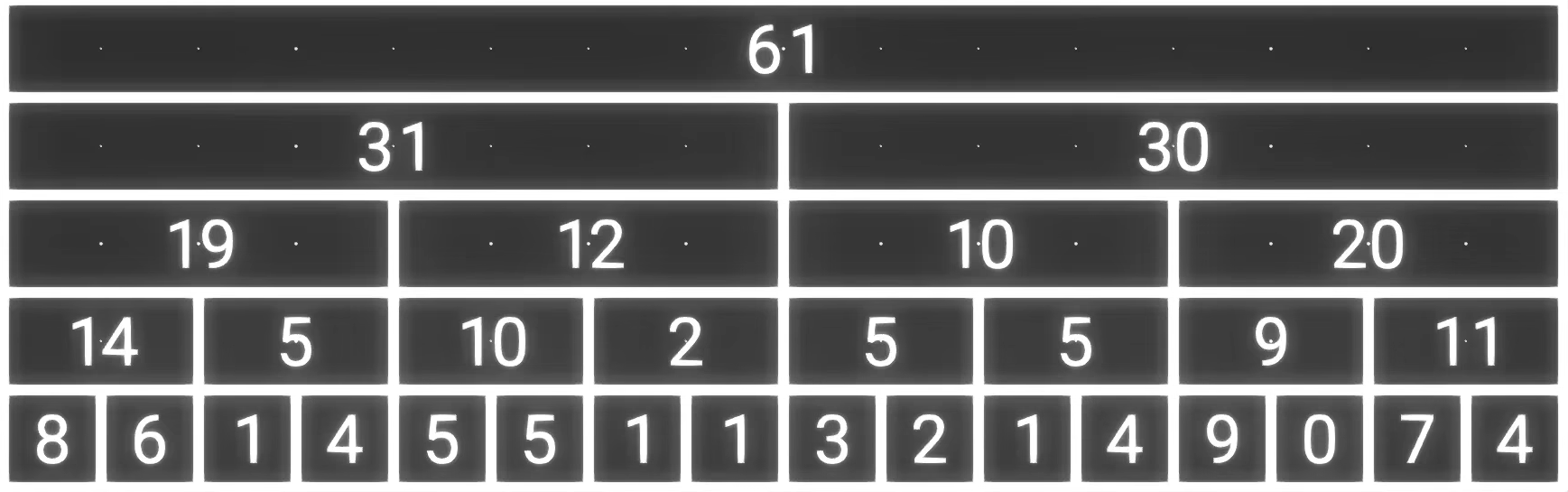
• 我们发现在我们进行修改和区间和的时候，有些元素是完全不会被用上的

  • 即：每行的第偶数个元素都是没必要的
  • 比如我们需要计算 $[1,3]$ 的区间和，我们只需要计算最下面数组的$a_3$ + 倒数第二行的 $a_1$ 即可。其余的都证明

• 所以我们将从上到下每个数组偶数个元素删去
  

• 发现剩下的数据正好有$n$个,即我们的新数组可以表示为一个为长度$n$的新数组，即树状数组

• 数组中的每一个元素，都代表莫一个区间
  

• 则我们可以在这个新的数组中了解树状数组两个操作，即单点修改和区间查询

• 那我们如何查找每个元素对应的区间呢？

  • lowbit(i)函数，这个函数会返回数 i 最后一位二进制为1的数对应的数 如 $5=(101{)}_2$ 则 lowbit(5)$=(1{)}_2=1$
  • lowbit(i){ return i&(-i);
  • 我们发现对上图的每个元素下标 $i$ ,$\mathrm{lowbit}(i)$ 即为从下到上的区间位置和区间长度
  • 也就是说，序号为$i$的序列正好就是长度为lowBit($i$)且以$i$结尾的序列。

回到引入题目，我们现在需要构建一个树状数组，那我们从树状数组的单点修改入手：

单点修改

• 当我们想要修改某一个数的时候，我们需要找到包含这个数的所有区间
  • 而树状数组的性质告诉我们，某一个序列上方的序列在树状数组的下标中为：$b[i^{\prime }]=b[i+\mathrm{lowbit}(i)$
  • 则我们只需要不断的向上累加直到超过长度就可以了
    

// 在i位置加k
void add(int i,int k)
{
	while(i < N){
		b[i] += k;
		i += lowbit(i);
	}
}

• 而对于初始化，我们只需要一开始设置一个长度为n，初始值0的数组,将每个$i$位加上元素值即可

void init()
{
	for(int i = 1 ; i <= n ; i++) add(i,v[i]);
}

Important

我们约定俗成的规定树状数组的下标由1开始，避免lowbit(0)的死循环问题

区间查询

• 树状数组能够做到的是对求到$i$的前缀和，而根据数上前缀和的原理，我们便可以求解区间
  • 前缀和的求解非常简单，只需要求i位置对应的区间及其前面的区间即可，可以用lowbit定位到每一个区间

int getsum(int i)
{
	int cnt = 0;
	while(i > 0){
		cnt += b[i];
		i -= lowbit(i);
	}
	return cnt;
}

• 而对于区间求和就可以使用数上前缀和的方法$ans=sum[r]-sum[l-1]$

int range_sum(int l ,int r)
{
	return getsum(r) - getsum(l-1);
}

Add

下面给出一个简单易于书写的fenwick数模板

struct fenwick{
	i64 n;
	vector<i64> bit;
	fenwick(i64 n): n(n) ,bit(n+1,0){}
	void add(i64 i,i64 v = 1){for(;i <= n;i += ( i & -i )) bit[i]+=v; }
	i64 sum(i64 i){i64 r = 0;for(;i >= 0;i -= i&-i)r += bit[i];return r;}
	i64 sum(i64 r,i64 l){return sum(r) - sum(l - 1);}
}