imicola's Blog

单调栈

5分钟阅读

模板 栈

单调栈

  • 何为单调栈？顾名思义，单调栈即满足单调性的栈结构。与单调队列相比，其只在一端进行进出。
  • 将一个元素插入单调栈时，为了维护栈的单调性，需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素。

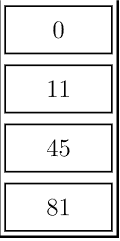
如上：一个 {0,11,45,81}的单调栈，如果要插入元素 14

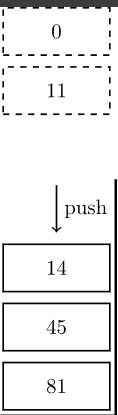
必须将{0,11} 弹出栈，再放入 元素 14

insert x;
while (!sta.empty() && sta.top() <= x) {
    sta.pop();
}
sta.push(x);

TIP

有的人会问，那被弹出去的元素呢？其实，在大部分单调栈问题中，我们更关注在一次弹出后的栈的状态，即在放入当前元素前栈的各个属性，比如：

  • 栈顶 能告诉我们比这个元素大(小)的元素是什么
  • 栈的大小 能告诉我们在这个元素前有几个比当前元素大(小)的元素

例题：

洛谷P5788 单调栈(模板)

signed main()
{
    //ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int t = 1;
    cin >> t;
    vint n(t);
    for (size_t i = 0; i < t; i++) {
        cin >> n[i];
    }
    stack<int> sta;
    vint result(t, 0);
    for (size_t i = t - 1; i >= 0; i--) {
        while (!sta.empty() && n[sta.top()] <= n[i]) {
            sta.pop();
        }
        result[i] = sta.empty() ? 0 : sta.top() + 1;
        sta.push(i);
    }
    for (auto &&i : result) {
        cout << i << " ";
    }
    return 0;
}

思路解释：

  • 维护一个单调存放数字下标的单调栈，这个单调栈入栈的规则根据数字的具体大小决定
  • 当某个元素入栈时，说明至少这个元素会比当前的栈顶下标所代表的元素要大，所以我们便把栈顶弹出，直到找到某个比当前元素大的数
  • 而找到的这个正好就是我们要找的刚好大于这个数，我们就被栈顶放入 result 数组中即可
  • 那为什么栈顶就是我们要找的数字呢？
    • 如 2 6 5 7 5
      • 进行比较的是与元素的大小，但栈存放的是下标 所以使用 n[sta.top()] <= n[i]进行下标栈和元素大小栈的转换
    • 我们最先放进去的是 5 ，此时栈的状态是 { 5 } ， 下标栈的状态 { 5 }
    • 接着我们要放入 7 ，不难发现 7 > 5 ,弹出 5 放入 7
    • sta : { 4 } —— num { 7 }
    • 再看 5 ，5 < 7 ,不需要弹出，直接放入，此时比 5 大的数就是 7 ，在result 数组下 放入 sta.top()即可
    • sta : { 3 4 } —— num {5 7}
    • 看 6 ，6 比 5 大 ，比 7 小 ， 将 5 弹出 ，放入 7 所代表的下标作为答案
    • 以此类推即可

例题2：

[USACO06NOV] Bad Hair Day S

signed main()
{
    //ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int t = 1, ans = 0;
    cin >> t;
    stack<int> cowh;
    for (size_t i = 1; i <= t; i++) {
        int h;
        cin >> h;
        while (!cowh.empty() && cowh.top() <= h) {
            cowh.pop();
        }
        ans += cowh.size();
        cowh.push(h);
    }
    cout << ans;
    return 0;
}

思路解释

  • 与上一题相似，但这次我们要找的是前面有多少个比放入的数字大的数量
    • 还是维护一个栈，如果当前放入的数字比栈顶大就弹出栈顶
    • 我们 ans 加的是还放入这个数的栈的大小，代表在这之前比这个数字大的数字有多少个
    • 我们要求的是 这个数能看见多少个数，求所有数能看见的总和 同样可以标识为 这个数能被多少个数看见，每个数能被看见的总和
    • 那当我们弹出比这个数小的数字之后，剩下的数就一定都能看见这个数
    • 将这些数量加到 ans 内即可

关系图谱