重积分

二重积分

• 直角坐标
  • 其重点在于将积分区域表示出来
  • 例：计算二重积分${\iint }_{D}xydxdy$，其中$D$由直线$y=2$,$x=2$,$y=2x$围成的有界闭区域。
  • 对积分区域$D$有
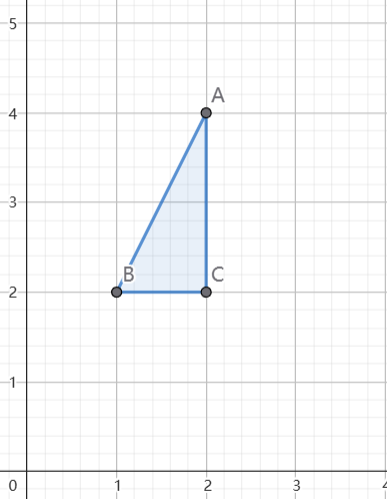
  • 此时我们可以将其看为x型(先y后x)的积分
  • ${\iint }_{D}xy\mathrm{d}x\mathrm{d}y={\int }_1^2\mathrm{d}x{\int }_2^{2x}xy\mathrm{d}y$
  • 在积后一个积分的时候就将x看为常量对y积分即可
• 极坐标
  • 利用极坐标变换：$\{\begin{array}{l}x=\rho \cos \theta \\ y=\rho \sin \theta \end{array}$
  • 当被积函数中含有 $x^2+y^2$ 这类式子时候或者积分区域是圆类时候可以使用极坐标变换
  • 极坐标变换注意$\mathrm{d}x\mathrm{d}y$要变为$\rho \mathrm{d}\rho \mathrm{d}\theta$
  • 设区域$D:x^2+y^2\le 1$，则积分${\iint }_D(xy+3{)}^{2}d\sigma =$
    • 利用极坐标变换有
    • ${\iint }_D({\rho }^2\cos \theta \sin \theta +3{)}^2\rho \mathrm{d}\rho \mathrm{d}\theta$
    • 在圆中 $\theta \in [0,2\pi ]\rho \in [0,r]$ $r$是圆半径
    • 有${\int }_0^{1}d\rho {\int }_0^{2\pi }({\rho }^2\cos \theta \sin \theta +3{)}^2\rho \mathrm{d}\theta$
    • BYD好难算放弃了
• 二重积分中值定理
  • 存在$(x_0,y_0)\in D$有${\iint }_{D}f(x,y)dxdy=f(x_0,y_0)\cdot S$
  • 其中S为D的面积
• 对称性
  • 二重积分区域$D$如果关于某一个变量轴对称，若其被积函数关于另一个变量为奇函数，则二重积分为0
    • 例：积分关于$x$轴对称，且$f(x,-y)=-f(x,y)$则该积分为0
  • 如果为偶函数，则只需要计算一半的区域然后乘2,即$2{\iint }_{D^{\ast }}f(x,y)dxdy$

三重积分

• 三重积分方法
  • 直角坐标计算法：先一后二与先二后一
    • 先一后二：即先计算一重积分，再计算二重积分
    • 常见形式 ：$z=x^2+y^2$ 与 $z=a$围的空间封闭区域
      • 将${\iiint }_{\Omega }f(x,y,z)dxdydz$ 化为${\iint }_{D}dxdy{\int }_{x^2+y^2}^{a}f(x,y,z)dz$
      • $D$为空间体在$xOy$平面上的投影
    • 先二后一：即先计算二重积分，再计算一重积分
      • 常见形式：当被积函数只有一个变量的时候，可以考虑后积这个变量。这样就可以化为：
      • ${\int }_{z_0}^{z_1}f(z)dz{\iint }_{D}dxdy={\int }_{z_0}^{z_1}f(z)\cdot Adz$
      • 其中$A$一般是一个可以用$z$表示的沿着$z$变化的面积
      • 如上例：若$f(x,y,z)=z$ ，则我们可以化为：${\int }_0^{a}z\cdot (\pi z)dz$
  • 球面坐标法
    • 球面坐标转换：
    • $\{\begin{array}{l}x=\rho \sin \varphi \cos \theta \\ y=\rho \sin \varphi \sin \theta \\ z=\rho \cos \varphi \end{array}$
    • 微元变化：$\mathrm{d}V={\rho }^2\sin \varphi \mathrm{d}\varphi \mathrm{d}\rho \mathrm{d}\theta$
    • $\rho$的范围:从原点出发的射线穿过区域的起点和终点对应的$\rho$值
      • 对于球体，通常是$0$到半径$R$;对于球壳，是内半径到外半径
    • $\varphi$的范围:从正$z$轴开始，向下扫描区域所需的角度范围
    • $\theta$的范围:在$xOy$平面上投影区域所覆盖的水平角度范围
  • 三重积分对称性
    • 三重积分区域$D$如果关于某两个变量平面对称(如$xOy$)，若其被积函数关于另一个变量为奇函数($f(x,y,-z)=-f(x,y,z)$)，则三重积分为0